Probability

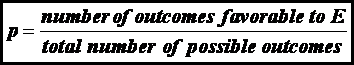
Before discussing statistical methods for dealing with measurements, it is useful to discuss the concept of probability. If there are several equally likely, mutually exclusive, and collectively exhaustive outcomes of an experiment, the probability p of an event E is

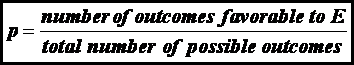
For example, when flipping a coin, there are two mutually exclusive, collectively exhaustive outcomes possible: heads and tails. The outcome will be either heads or tails (mutually exclusive) and there is no possible outcome other than heads or tails (collectively exhaustive).[1] If a coin and coin flipper are unbiased, there is an equal probability of either outcome. How can we determine the probability of a more complex outcome - for example, the probability of obtaining 3 straight “heads”?

On the first flip, heads (H) and tails (T) are equally probable. There is one possible favorable outcome (H) out of two possible outcomes total. Each flip has either (H) or (T) as a possibility. What combinations are possible in 3 flips of the coin? HHH, HHT, HTH, HTT, TTT, TTH, THT, THH are the only possible outcomes of 3 flips of the coin. 1 favorable outcome out of 8 possible outcomes: p = 1/8; 0.125 or 12.5%.

What is the probability of 2 consecutive heads in 3 flips? p = 3/8; 0.375 or 37.5%.

Now let’s play cards. We’ll use a standard deck of 52 cards (no jokers). The probability of drawing a specific card (ace of diamonds) is 1 in 52. The probability of drawing any ace is 4 in 52. What is the probability of drawing two aces from the deck in the first two consecutive draws?

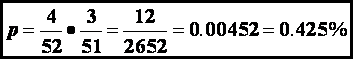
The probability of drawing the first ace is 4 in 52. The probability that the second card drawn from the deck is an ace is 3 in 51 if the first card drawn was an ace. If the first card drawn was not an ace, the probability of drawing an ace in the second draw is improved to X in 51, but chances for a favorable outcome (pair of aces) has already vanished. We obtain the probability of a compound event (A and B) by multiplying the probabilities of each event:

What are the odds of 3 straight wins in roulette? If the wheel has 37 slots, with each outcome equally probable (we assume an honest game).

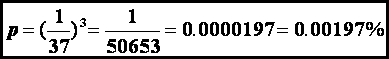
Casinos are profitable for the operators because probability in on the side of The House for all casino games, even when played honestly.[2] The only casino game where players can win in the long run is Black Jack, and then only if a player can keep track of cards played from the shoe. By counting how many of certain cards have been dealt, card counters can improve their take by betting heavily when the deck is rich in cards unfavorable to the house. Of course, casinos prohibit card counting and eject players who appear to be card counting (in other words, regular winners at the black jack table).

[1] Some of these concepts are from Mathematical Methods in the Physical Sciences by Mary L. Boas; John Wiley and Sons, New York , 1966. Others are from Applied Statistics for the Behavioral Sciences by Hinkle, Wiersma and Jurs, Houghton Mifflin, Dallas, 1979.

[2] I do not understand how rational people think they can beat video poker or Internet games involving wagers. These games are easily fixed so that the operator wins all of the large bets. How do you prevent a computer program from dealing electronic cards from the bottom - or the middle, for that matter - of the deck? Neither do I understand how William Bennett, Secretary of Education under President Reagan, managed to lose $8,000,000 in casinos. How can someone who should understand probability well enough to interpret statistics about student test scores delude himself into thinking that he can beat the laws of probability?