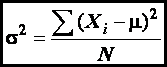The range of a set of values is the difference between extreme values (highest and lowest) plus 1.  The range of series S = (10 - 4 + 1) = 7.  

            Variance is a measure of the dispersion a set of values.  The variance of a population (σ²)  is defined as

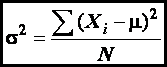   (2)

where N is the number of members of the population, μ is the mean value, and X_i is the value of the i^th member.  The variance of a sample (s²) is defined as

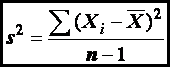   (3)

where X-bar (X with the line over it) is the mean of the sample, and n is the number of values in the sample.  

            It is my understanding that a "population" involves all (for example, all residents of Toledo : N = population of Toledo ) while a "sample" represents a subset of a recognized larger set (2000 random individuals selected from the residents of Toledo : n = 2000).  

            Random errors scattered about a mean frequently exhibit a normal distribution.  There are more values close to the mean than far from the median.  A normal distribution describes data or measurements that are consistent with the equation

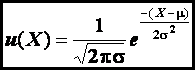   (4)

where u is the value of the function, μ is the mean (equation 1), and σ is the standard deviation (equation 5 or equation 6). 

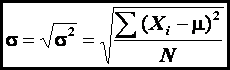   (5)

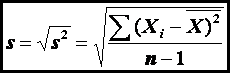   (6)

Of course, s replaces σ when characterizing a sample rather than a population.

            Equation 4 describes the bell curve, the graph consistent with a normal distribution.

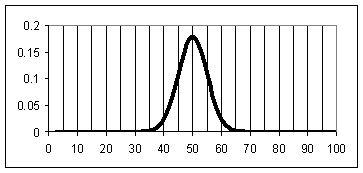
Figure 1: bell curve for mean = 50 and standard deviation = 5.0.

Figure 1 is an example of a bell curve.  Compare Figure 1 with Figure 2, a distribution with the same mean but a larger standard deviation.

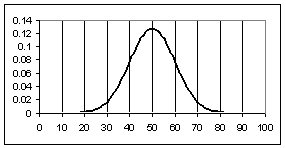
Figure 2: Bell curve for mean = 50 and standard deviation = 10.

The area under a segment the bell curve represents the percentage of a population or sample that falls within the range of that segment.  The area between the mean and one standard deviation above or below the mean equals 34.13% of the total area.  The area between the mean and two standard deviations equals 47.72%, and the area between the mean and three standard deviations equals 49.87%.  

Given a set of measurements subject to random error, the standard deviation provides a measure of the confidence we might have that the "true" value lies within a certain range.  Confidence is 68% that the true value lies within 1 standard deviation of the mean (in Figure 2, between the values 40 and 60).  Confidence is 95% that the true value lies within 2 standard deviations (between 30 and 70 in Figure 2) and 99% that it lies within 3 standard deviations (between 20 and 80).  

            Most "scientific" calculators have built-in statistical functions.  You will probably have to locate the manual and look up the procedure for entering data and accessing the results (mean, standard deviation).

Return to Dose of Statistics